Regresión lineal múltiple
Introducción
La estadística multivariable es una rama de la estadística donde se intenta explicar un fenómeno de salud teniendo en cuenta varias variables de cualquier tipo (cuantitativas, ordinales, cualitativas etc.)1. Por ejemplo, supongamos que realizamos una investigación para conocer el efecto que tienen fumar en el embarazo, el peso de la madre, la presencia de comorbilidades y el uso de medicamentos sobre el peso del recién nacido. En este ejemplo, nuestra variable dependiente es el peso al nacer e intentamos explicar como influyen el resto de las variables (variables independientes). Otro ejemplo de le estadística multivarible podría ser el estudio de variables asociadas a tensión arterial, en el que se podría incluir variables como consumo de sal, edad, sexo, la presencia de comorbilidades y el habito de fumar. Utilizando la estadística multivariable se podría conocer cual es el efecto de todas estas variables juntas sobre la tensión arterial. También, con estadística multivariable podemos aislar el efecto de una variable sobre otra, por ejemplo, podríamos aislar el efecto del consumo de sal sobre la tensión arterial, teniendo en cuenta el resto de las variables.
Dos de las pruebas estadísticas multivariables más utilizadas son la regresión lineal múltiple y la regresión logistica multivariable. Aquí nos enfocaremos en la regresión lineal múltiple.
Martínez González y cols. en su libro Bioestadística amigable 2 describe los usos que pueden tener los modelos de regresión multivariable. Se muestra un extracto de este tema en los siguientes puntos:
“Determinar cuáles son los predictores de una variable biosanitaria (variable Y, o variable dependiente) a partir de una lista más o menos amplia de posibles variables predictoras o explicativas (variables X o variables independientes). Por ejemplo, de un listado de 20 posibles polimorfismos genéticos, ¿cuántos y cuáles de ellos son capaces de predecir en más o menos grado la probabilidad de ser obeso? ¿Cuál será la probabilidad de ser obeso si se posee el polimorfismo A? ¿Y si se tienen los polimorfismos A y B? ¿Y si se poseen los polimorfismos A, B y C?”
“Construir un índice pronóstico (ecuación) para predecir una determinada condición (variable Y) a partir de los valores recogidos en un conjunto de variables (variables X). Por ejemplo, predecir la probabilidad de que un paciente presente enfermedad coronaria en los siguientes 10 años conociendo su sexo, su edad, el nivel de colesterol, la tensión arterial y el hábito tabáquico (ecuación de Framingham)”.
“Determinar el efecto de una variable X1 sobre otra variable Y teniendo en cuenta otras características (X2, X3… Xp; factores de confusión) que pudieran que pudieran distorsionar la verdadera asociación entre estas variables. Por ejemplo, determinar el efecto del consumo de comida rápida sobre el riesgo de desarrollar depresión, considerando la cantidad de actividad física realizada por el individuo y su hábito tabáquico”.
“Detectar y describir fenómenos de interacción entre variables (modificación del efecto) sobre un determinado resultado. Es decir, si la presencia de una variables X2 es capaz de modificar el efecto ejercido por la variable independiente X1 sobre la variable dependiente Y. Por ejemplo, se desea determinar si el efecto del consumo de una dieta rica en grasas saturadas sobre el cambio de peso es diferente según exista o no presencia de un determinado polimorfismo genético”.
Por otro lado, la estadística multivariada, hace referencia a la aplicación de técnicas estadísticas a conjuntos de datos que involucran más de una variable dependiente3. En este caso, se busca determinar la relación entre las variables dependientes y las variables independientes. Posteriormente nos enfocaremos en estos temas.
Regresión lineal múltiple
Modelo de regresión lineal múltiple
El análisis de regresión múltiple se puede interpretar como una ampliación de la regresión lineal cuando incluye más de una variable independiente. Así, el modelo general para k variables independientes se expresa de manera simplificada como:
\[Y=\beta_0+\beta_1X_1++\beta_2X_2+...\beta_kX_k+\epsilon\]
Donde:
\(\beta_0\), \(\beta_1\), \(\beta_2\)…\(\beta_k\) son los coeficientes de la regresión para el intercepto y para cada uno de las variables.
\(X_1, X_2, X_k\) son las variables independiente.
Conceptos sobre regresión lineal múltiple
Antes continuar con la realización de los modelos de regresión lineal múltiple, es necesario revisar algunos conceptos claves para entender el modelo de regresión múlitple.
Variables dummy.
En un modelo de regresión múltiple es posible incluir variables categóricas, sin embargo, su inclusión requiere la creación de variables dummy. La creación de este tipo de variables para poder ajustar los modelos con aquellas variables categóricas que tienen más de dos niveles.
“Si la variable categórica está formada por \(k\) categorías, será posible analizarla introduciendo en el modelo simultáneamente \(k−1\) variables dummy. Estas variables ficticias son dicotómicas y toman los códigos 0 y 1. El valor 0 se asigna a aquella categoría que se toma como referencia, y habrá una variable dummy por cada una de las otras categorías, que solo valdrán 1 cuando el sujeto pertenezca a la respectiva categoría. Generalmente se asigna el valor 0 a aquella categoría en que se espera un nivel menor o basal” Fragmento de Bioestadística amigable (Spanish Edition) 4.
Algo que se debe tener en cuenta cuando se crean las variables dummy, es que estas solo tienen sentido cuando se analizan en conjunto, nunca deben de analizarse por separado. Fuera de un modelo de regresión o un modelo de machine learning, las variables dummy no tienen sentido.
Supongamos que queremos realizar un modelo en el que se incluya una variable relacionada al hábito de fumar. Esta variables contiene los siguientes niveles:
- No fumador
- Ex-fumador
- Fumador.
La creación y por tanto la introducción de esta variable al modelo requerirá de la creación de dos variables dummy (\(k−1\)) donde cero es la ausencia del evento. La siguiente tabla muestra la creación de estas variables:
| X1 | X2 | |
|---|---|---|
| No fumador | 0 | 0 |
| Ex fumador | 1 | 0 |
| Fumador | 0 | 1 |
En la tabla anterior podemos identificar que uno de lo niveles sirve para comparar a las otras dos y funciona como un estado basal. Podemos comparar la ausencia (no fumador) con la variable X1 (ex fumador) y la ausencia del viento (no fumador) con X2 (fumador). Esta explicación la podemos trasladar a los coeficientes de la regresión.
Interpretación Coeficientes \(\beta\) en la regresión lineal
Al igual como sucede en la regresión lineal simple, en los resultados de la regresión lineal múltiple podemos obtener coeficientes \(\beta\) de la regresión para cada una de las variables. Pero su interpretación es un poco distinta. Existe un coeficiente \(\beta\) (pendiente) para cada variable. Así por ejemplo, una regresión con 5 variables predictores tendrá 5 pendientes. Cada coeficiente se interpretará como el cambio en la variable dependiente por una unidad de cambio en una de las variables predictores sin tener en cuenta las demás. Esta interpretación de \(\beta\) solo es correcta cuando se asila el efecto de una variable y no se toma en cuenta las demás. Además, es imposible interpretar una regresión si no se conocen las unidades de medida de cada variable. Esto se aplica tanto a la regresión simple como a la múltiple.
Suponga que tenemos una regresión múltiple en la que nuestra variable dependiente es el peso al nacer de un grupo de recién nacidos medidos en gramos. Este modelo se ajustó por la edad de la madre, el peso de la madre y el consumo de tabaco (no fumador, ex fumador y fumador). La edad se expresa en años, el peso de la madre en kilos y el consumo de tabaco como un factor de tres niveles.
La siguiente tabla muestra los resultados del ANOVA para esta regresión.
| Estimate Std. | Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 1.08572 | 0.20398 | -20.872 | 4.61e-09 *** |
| Edad | -0.70000 | 0.0145 | 38.628 | < 2e-16 *** |
| Peso _Madre | 20.34 | 0.18676 | -3.473 | < 2e-16 *** |
| ex-fumador | -30.4 | 0.20398 | -20.872 | < 2e-16 *** |
| Fumador | 40.8 | 0.01293 | -10.234 | < 2e-16 *** |
El ANOVA para la variable edad indica un coeficiente \(\beta\) de -0.70. Esto indica que por cada año que cumplan la madres se observará una disminución de 0.70 gramos en el peso del bebé. Siempre y cuando no existan modificaciones del resto de las variables. Para la variable peso de la madre se obtuvo un coeficiente de 20.34, este coeficiente indica que por cada kilo de peso que aumente la madre se observará un aumento de 20.34 gramos en el peso del recién nacido. Siempre y cuando no cambie ninguna de las otras variables.
Para la variable de consumo de tabaco, podemos observar que para la primer variable dummy que corresponde para el nivel de ex fumador tenemos un valor de \(\beta\) de -30.4, lo cual indica que comparado con el estado basal (no fumador) hay una disminución de 30.4 gramos en el peso del recién nacido. Siempre y cuando no cambien ninguna de las otras variables. Para el nivel de fumador se obtuvo un valor de \(\beta\) de -40.8, lo cual indica que los hijos de las madres que fuman tienen una disminución en el peso de 40.8 comparado con la madres que no fuman. Siempre y cuando no existan cambios
Intervalos de confianza
La interpretación de los intervalos de confianza para los coeficientes es el mismo que para la regresión lineal simple. Se busca que el coeficiente sea distinto de cero.
Coeficiente de determinación ajustado
Cuando al modelo de regresión se añaden variables este coeficiente tiende a aumentar, por lo que este coeficiente requiere de ajustes para su correcta interpretación. La formula siguiente representa la estimación para el coeficiente de determinación ajustado.
\[R_{adj}^2=1-\bigg[\frac{(1-R^2)(n-1)}{n-k-1}\bigg]\]
Se podría decir que el coeficiente de determinación es el porcentaje que explica el modelo. Por ejemplo, con un coeficiente de 0.70, se podría decir que el modelo explica un 70% de lo que sucede con la variable dependiente dadas las variables independientes.
En el caso de la regresión linela múlitple si no se ajusta el valor de \(R^2\) es posible que se sobreestime la capacidad explicativa del modelo. Esto ocurre porque el \(R^2\) tradicional sin ajustar tiende a aumentar conforme se añaden más variables al modelo, incluso si esas variables no aportan información relevante para explicar la variable dependiente. El \(R^2\) ajustado, por otro lado, corrige este problema al penalizar el número de predictores incluidos, proporcionando una medida más precisa del poder explicativo del modelo
No ajustar el valor del coeficiente de determinación sería un error que exageraría “lo que explica en modelo”
No olvidemos que también en el caso de la regresión múltiple es necesaria la realización de un ANOVA para evaluar si el modelo pudiera ser útil.
Supuestos para la aplicación del modelo de regresión lineal múltiple.
En el caso de la regresión lineal múltiple debemos de cumplir con los mismos supuestos que se revisaron en el tema de regresión lineal simple.
- Las variables están relacionadas linealmente.
- La distribución de la variable dependiente condicionada a cada posible combinación de valores de las independientes es una distribución normal multivariable.
- Las observaciones para cada variable son independientes unas de otras. No existen dos observaciones autocorrelacionadas entre sí (p. ej., observación ojo derecho/ojo izquierdo del mismo individuo).
- Existe homogeneidad de las varianzas (homocedasticidad): las varianzas de la variable Y condicionadas a los valores de X son homogéneas.”
- No debe presentarse multicolinealidad entre las variables independientes.
Multicolinealidad
Un punto importante que se de debe tomar en cuenta es que las variables no deben de presentar colinealidad, es decir no deben de estar autocorrelacionadas entre si. Dos variables independientes altamente correlacionadas entre si, modificarán de forma crítica los coeficientes \(\beta\). Una alta colinealidad produce:
- Inestabilidad en los coeficientes: Los coeficientes estimados de las variables correlacionadas pueden volverse muy inestables. Un pequeño cambio en los datos puede llevar a grandes variaciones en los coeficientes, lo que dificulta interpretar correctamente la relación entre las variables independientes y la variable dependiente.
- Pérdida de significancia estadística: A pesar de que las variables incluidas podrían ser importantes para el modelo, la multicolinealidad puede hacer que pierdan significancia estadística (es decir, altos valores de p), lo que lleva a la interpretación errónea de que esas variables no son útiles para el modelo.
- Difícil interpretación de los coeficientes: Debido a la alta correlación entre las variables, se vuelve complicado interpretar los coeficientes de cada una de ellas. Es difícil distinguir el impacto de una variable independiente en la variable dependiente sin que esté influenciado por la otra variable correlacionada.
- Aumento de los errores estándar: La multicolinealidad incrementa los errores estándar de los coeficientes, lo que reduce la precisión de las estimaciones.
Evaluación de la colinealidad
La colinealidad (o multicolinealidad, en el contexto de múltiples variables predictoras) se refiere a la situación en la cual dos o más variables predictoras en un modelo estadístico están altamente correlacionadas, es decir, tienen una relación lineal entre sí.
Existen dos formas de evaluar la colinealidad. La primera es realizando una matriz de correlación; y la segunda es evaluando factor inflación o incremento de la varianza (VIF)
En la caso de realizar una matriz de correlación puede proceder conforme a lo revisado en clase. Otra opción es utilizar la función corrplot.mixed de la librería cor. Esta función requiere un data frame con variables de tipo numérico o en su defecto, un data frame con las variables que serán evaluadas en el modelo.
La siguiente opción es utilizar el VIF. El VIF se define como la proporción de variabilidad de la variable \(X_i\) que es explicada por el resto de las variables predictoras del modelo. Cuando el VIF, crece, también lo hace la varianza del coeficiente de regresión, y el modelo se vuelve inestable. Si los valores del VIF, fuesen grandes, serían un indicador de la existencia de multicolinealidad. Valores entre 5 y 10 indican posible presencia de colinealidad. Mayores a 10 indican alta colinealidad.
Para evaluar el VIF, se puede utilizar la función vif de la librería car. Esta función requiere de un modelo de regresión lineal múltiple.
Cómo lidiear con la multicolinealidad
- Eliminar una de las variables altamente correlacionadas para reducir la redundancia.
- Usar técnicas de regularización como Ridge o Lasso, que penalizan los coeficientes para mitigar el impacto de la multicolinealidad.
- Transformar las variables en combinaciones lineales, como a través del Análisis de Componentes Principales (PCA), para reducir la colinealidad. Este punto se revisará en clase más adelante.
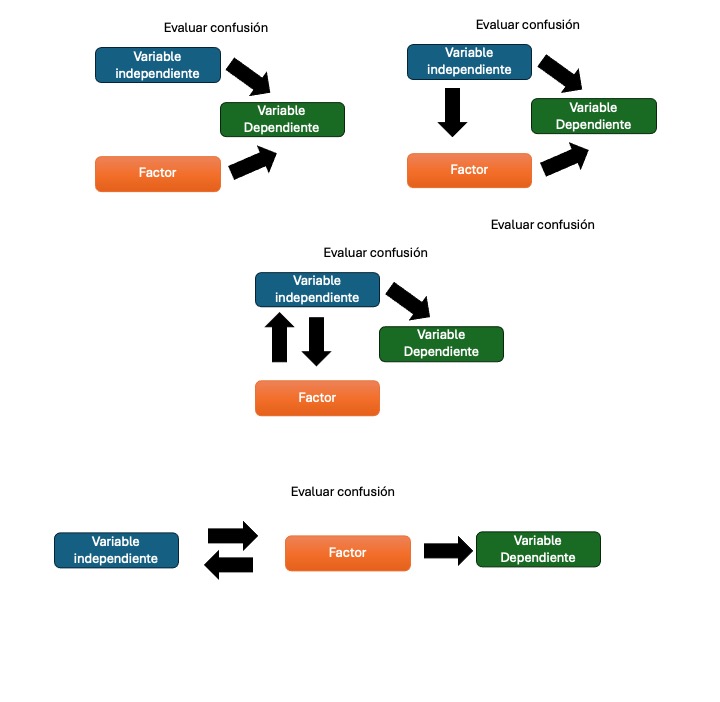
Variables confusoras
Una variable confusora es una variable que se encuentra relacionada tanto con la variable dependiente como con alguna o varias de las variables independientes.
El resultado de la presencia de una variable de confusión puede ser desde la perdida de asociación hasta la exageración de esta asociación.
Incluso en algunos casos se puede invertir el sentido de la asociación. La identificación de una variable de confusión requiere de experiencia y de conocimiento sobre el tema. Por ejemplo, para considerar una variable como confusora deberá, entre otras cosas, estar asociada con el efecto y con la exposición de forma independiente y no estar condicionada por la presencia del mismo. Además nunca una variable de confusión deberá evaluarse únicamente utilizando valores de p, sino que deberá evaluarse la magnitud del efecto. Se considera como valido un cambio mayor al 10% en el cambio del coeficiente.
El modelo correcto siempre es el que se ajusta por la variable confusora.
La siguiente figura muestra un ejemplo de cuando evaluar una variable confusora.
Footnotes
Hidalgo B, Goodman M. Multivariate or multivariable regression? Am J Public Health. 2013 Jan;103(1):39-40. doi: 10.2105/AJPH.2012.300897. Epub 2012 Nov 15. PMID: 23153131; PMCID: PMC3518362.↩︎
Martínez-González, M. A., & Martínez-González, M. A. (2011). Bioestadística amigable. Elsevier España.↩︎
Hidalgo B, Goodman M. Multivariate or multivariable regression? Am J Public Health. 2013 Jan;103(1):39-40. doi: 10.2105/AJPH.2012.300897. Epub 2012 Nov 15. PMID: 23153131; PMCID: PMC3518362.↩︎
Martínez-González, M. A., & Martínez-González, M. A. (2011). Bioestadística amigable. Elsevier España.↩︎